La ley de la gravitación universal fue publicada por Isaac Newton en 1687 en su obra Principios matemáticos de filosofía natural y se expresa con la siguiente afirmación: “toda partícula del universo atrae a toda otra partícula con una fuerza que es directamente proporcional al producto de sus masas, e inversamente proporcional al cuadrado de la distancia entre ellas” (Serway, Jewett, 2006).
En el análisis espacial de la movilidad de personas y carga es común la utilización del paradigma gravitacional para modelar las interrelaciones entre los orígenes y destinos de los viajes y estimar la intensidad del transporte que tendrá lugar entre diversos puntos del espacio geográfico.
Los modelos gravitacionales se basan en el principio de que la intensidad de la interacción entre dos localidades es una variable directamente proporcional a la importancia relativa de éstas, e inversamente proporcional al esfuerzo necesario para desplazarse entre ellas. Es así como la importancia en un área geográfica "atrae" viajes, de un modo semejante a como los objetos son atraídos por la fuerza de gravedad en el espacio.
El esfuerzo requerido para superar el espacio geográfico se ha estimado tradicionalmente mediante la distancia física que las separa (longitud del viaje), suponiendo implícitamente que hay una relación directamente proporcional entre esfuerzo y distancia, y que el espacio geográfico es homogéneo en términos de accesibilidad (Seguí, Martínez; 2004). De forma simple, el modelo gravitacional, las zonas "más grandes" obtienen más viajes (atracción) mientras que los destinos más cercanos (impedancia) obtienen más viajes.
Esencialmente, las producciones de una zona se asignan a todas las demás zonas en relación con la utilidad de cada zona desde el origen. La utilidad son las atracciones en la zona de destino multiplicadas por la impedancia de la zona de origen a la zona de destino. Recordar que la impedancia es un valor negativo.
Donde
Pi= Zona de producción i
Aj= Zona de atracción j
Fij= Impedancia desde Zona i a Zona j
Para cada zona de origen, la utilidad se calcula para cada zona de destino y luego se suma. Esto representa una utilidad total de todos los destinos desde el origen. Cada utilidad de zona de destino se divfide por la utilidad total para todas las zonas, lo que da como resultado una probabilidad. El paso final es entonces, para cada zona de origen, multiplicar las producciones por las probabilidades. (Una para cada zona de destino) para obtener la distribución del viaje. El resultado es una matriz de viajes para todos los pares de zonas.
La matriz que se produce a partir del proceso descrito anteriormente es una matriz restringida individualmente. Hay tres tipos de matrices restringidas:
- Producción restringida: Los valores de la suma de la matriz a los objetivos de la fila (producción)
- Atracción restringida: Los valores de la suma de la matriz a los objetivos de columna (atracción)
- Producción y atracción restringida: Son matrices doblemente restringidas porque los valores de la matriz se suman lo mejor posible a los objetivos de la fila (producción) y columna (atracción)
Una matriz restringida individualmente es aquella que respeta los totales de control de una de las dimensiones (fila o columna). En el ejemplo anterior, el resultado es una matriz restringida de producción. Esto significa que las producciones están satisfechas, es decir, todas las producciones generadas en el paso de generación de viajes se asignan a las zonas de destino. Sin embargo, los viajes sumados a las columnas (como atracciones) pueden no respetar los totales de la etapa de generación. Lo que se necesita es una matriz doblemente restringida, una que respete ambos objetivos. Para lograr una matriz doblemente restringida, se necesita un método iterativo. El método son los modelos de factores habituales. El resultado es un método que utilice factores de crecimiento. Una matriz con las sumas de la fila y las sumas de columna siendo iguales a los objetivos, y la suma de las sumas de la fila y la suma de las sumas de la columna siendo iguales.
El modelo gravitacional es típicamente el modelo más popular aplicado en la distribución de viajes, pero se enfrenta a ciertos problemas, entre ellos, que cuando existe una baja correlación entre la población de un área geográfica y la movilidad, estos modelos tienen dificultades para ser confiables en la estimación de viajes realizados. Es así como otros autores han propuesto nuevos modelos de transporte más exactos e incluso, adaptados a diferentes conextos. En el futuro, estaremos hablando de ellos.
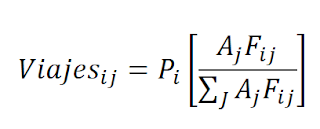
Comentarios
Publicar un comentario